Symulacja równowagi utleniania – redukcji za pomocą MS Excela cz. IV
Miareczkowanie redoksometryczne
lab_lab_lab_lab_lab_lab_lab_lab_lab_lab_lab_lab_lab_lab_labWaldemar Ufnalski*
Niniejszy artykuł jest kontynuacją cyklu, rozpoczętego w numerze LAB 6/2001, mającego na celu zaznajomienie Czytelników z obliczeniami i symulacjami „chemicznymi” za pomocą arkusza kalkulacyjnego MS Excel® i zgodnie z przyjętymi założeniami dołączono do niego oprogramowanie i skoroszyty z przykładami.
Pojęcia podstawowe i przyjęty model omówiono w poprzednich trzech artykułach wchodzących w skład tego cyklu [1,2,3]; niniejszy artykuł kończy cykl poświęcony równowagom utleniania – redukcji. Odwołania do wzorów podanych w [3] będą oznaczane „[3] – numer wzoru”.
Sformułowanie zadania
Rozróżnia się miareczkowanie oksydymetryczne polegające na miareczkowaniu roztworu oznaczanego reduktora – roztworem mianowanego utleniacza oraz miareczkowanie reduktometryczne polegające na miareczkowaniu roztworu oznaczanego utleniacza – roztworem mianowanego reduktora. Algorytm obliczeniowy jest dla obu wariantów praktycznie identyczny i załączone oprogramowanie obsługuje oba warianty, rozpoznając programowo właściwy wariant. Postęp miareczkowania śledzi się potencjometrycznie lub kolorymetrycznie za pomocą barwnych wskaźników redoks; załączone oprogramowanie generuje krzywą miareczkowania w układzie współrzędnych „objętość roztworu titranta – potencjał względy sondy Pt”.
Do obliczeń zastosowano omówiony w [3] algorytm stechiometryczny oparty na modelu elektrochemicznym; obowiązują nadal przyjęte uprzednio ograniczenia. Przypomnijmy te, które są istotne podczas symulacji miareczkowania oksydymetrycznego
(dla miareczkowania reduktometrycznego będą one „symetryczne”).
- Oznaczany reduktor i titrant – utleniacz muszą być składnikami roztworu.
- Utleniacze i reduktor będące produktami reakcji mogą być ewentualnie fazami czystymi (gazem wydzielającym się z roztworu lub strącającym się osadem np. tlenku metalu).
- Ten sam utleniacz lub reduktor będący składnikiem roztworu nie może występować równocześnie w równaniach obu reakcji połówkowych. Ograniczenie to nie dotyczy reagentów będących fazami czystymi (gazem, kryształem).
Warto chyba dodać krótkie wyjaśnienie ostatniego ograniczenia. W dosyć nielicznych przypadkach oznaczeń redoksometrycznych sumaryczna reakcja utleniania – redukcji polega na zmianie stopnia utlenienia tylko jednego rodzaju atomów
(symproporcjonowaniu). Na przykład oznaczanie manganu metodą manganometryczną Volharda [4] polega na miareczkowaniu roztworu zawierającego oznaczany pierwiastek w postaci kationu Mn
2+, mianowanym roztworem nadmanganianu potasu w środowisku obojętnym. Reakcja sumaryczna jest opisana równaniem
(1)
Można ją wygenerować zakładając równania reakcji potencjałotwórczych
(2a)
(2b)
Ten model elektrochemiczny można przenieść „do kolby w której zmieszano oba substraty” gdyż w obu półogniwach nie ma takich samych składników roztworu będących utleniaczami lub reduktorami a reagent wspólny
(MnO2(s)) jest substancją czystą Załączone oprogramowanie poprawnie obliczy położenie stanu równowagi „w kolbie” i wygeneruje krzywą miareczkowania.
Formalnie równanie sumaryczne (1) można też wygenerować zakładając równania reakcji potencjałotwórczych
(3a)
(3b)
Takiego modelu elektrochemicznego nie można jednak przenieść „do kolby w której zmieszano oba substraty”; po wyrównaniu potencjałów półogniw
(„osiągnięciu stanu równowagi przez „rozładowanie ogniwa”) stężenia równowagowe jonów Mn
2+ w obu półogniwach są różne i układ nie jest równoważny termodynamicznie „roztworowi w kolbie”.
Oto zwięzły opis postępowania w celu wygenerowanie krzywej miareczkowania. Założono, że lewe półogniwo zawiera oznaczany reduktor
(RL), natomiast prawe półogniwo zawiera utleniacz – titrant
(UP).
- Ustala się równania reakcji połówkowych i przypisuje im potencjały standardowe.
- Zakłada się objętość
roztworu miareczkowanego zawierającego roztwór oznaczanego reduktora RL o stężeniu początkowym
oraz zakłada się stężenie (miano) roztworu utleniacza – titranta.
- Oblicza się się stężenia „początkowe” RL i UP po dodanu
roztworu titranta
(4a)
(4b)
Stężenia początkowe UL oraz RP są w założeniu równe zeru (jest to założenie sensowne, odpowiadające procedurze doświadczalnej; dla programu nie jest ono konieczne).
- Po podstawieniu (4a/b) do ([3]-29) można wyrazić stężenia wszystkich reagentów (składników roztworu) za pomocą współrzędnej reakcji([3]-28). Podstawienie ich do wzoru ([3]-27) daje rozwiązywane równanie; po jego numerycznym rozwiązaniu oblicza się stężenia równowagowe reagentów a następnie potencjał równowagowy.
- Zmieniając objętość dodawanego roztworu titranta z dostatecznie małym krokiem generuje się kolejne punkty na krzywej miareczkowania.
Jeżeli w przypadku ogólnym równania połówkowe mają postać
(5a)
(5b)
to, przy założeniu
, sumaryczne równanie ma postać
(6)
Bilans ładunku zapewniono mnożąc każde równanie razy liczbę ładunkową drugiego równania połówkowego.
Stechiometryczne stężenie roztworu titranta (UP) dane jest więc wzorem
(7)
W takim przypadku PR zostajnie osiągnięty po zmieszaniu identycznych objętości roztworu, w którym oznaczamy RL i roztworu titranta UP.
Jeżeli współczynniki stechiometryczne wszystkich utleniaczy i reduktorów w równaniach (5a/b) są równe jedności i wszystkie utleniacze i reduktory są składnikami roztworu, to potencjał w punkcie równoważnikowym można wyrazić wzorem:
(8)
Wyprowadzenie wzoru (8) można znaleźć w wielu podręcznikach akademickich np. [4], [5]. Niestety Autorzy podręczników (przejrzanych przeze mnie) sugerują ogólność wzoru (8), który w rzeczywistości dotyczy układów szczególnego typu – nazwanego przeze mnie (nie jest to termin powszechnie przyjęty) „układem symetrycznym”.
Oprogramowanie przeznaczone do generowania krzywych miareczkowania
Do programów opisanych w [1] , [2] i [3] dołączono następujące funkcje umieszczone w dodatku LABREDOX.XLA:
- RedOx_Objetosc_Rownowazna_Prawego_cm3(L_Eform_mV, L_Licz_Lad_mol,
L_Kody_Skladn, L_Kody_Faz, L_Wsp_Stechiom,
L_C0_mol_dm3, L_V0_cm3,
P_Eform_mV, P_Licz_Lad_mol,
P_Kody_Skladn, P_Kody_Faz, P_Wsp_Stechiom,
P_C0_mol_dm3,
Temperatura_K) – funkcja zwraca objętość roztworu titranta niezbędną do osiągnięcia PR. Przed obliczeniem sprawdza zbieżność procedury generującej krzywą miareczkowania. Parametr rozpoczynający się literą L_ dotyczy półogniwa lewego, natomiast P_ - prawego. Ostatni parametr jest opcjonalny – wartością domyślną jest 298,15 K.
- RedOx_Krzywa_Miarecz_Potencjal_mV(L_Eform_mV, L_Licz_Lad_mol,
L_Kody_Skladn, L_Kody_Faz, L_Wsp_Stechiom,
L_C0_mol_dm3, L_V0_cm3,
P_Eform_mV, P_Licz_Lad_mol,
P_Kody_Skladn, P_Kody_Faz, P_Wsp_Stechiom,
P_C0_mol_dm3, P_V_cm3,
Temperatura_K) - zwraca potencjał sondy po doda¬niu P_V_cm3 roztworu titranta.
- RedOx_Krzywa_Miarecz_Stezenia_Form_mol_dm3 (L_Eform_mV,
L_Licz_Lad_mol, L_Kody_Skladn, L_Kody_Faz, L_Wsp_Stechiom,
L_C0_mol_dm3, L_V0_cm3,
P_Eform_mV, P_Licz_Lad_mol, P_Kody_Skladn, P_Kody_Faz,
P_Wsp_Stechiom P_C0_mol_dm3, P_V_cm3, Temperatura_K) – funkcja tablicowa (tablica pozioma czteroelementowa) zwraca stężenia wszystkich utleniaczy i reduktorów po dodaniu P_V_cm3 roztworu titranta w kolejności: UP, RL, RP, UL.
Symulowanie i badanie krzywych miareczkowania
Badanie krzywych miareczkowania warto rozpocząć od symulacji prostych układów modelowych – oto kilka propozycji.
Przykład 1. Krzywe miareczkowania układów modelowych – układy „symetryczne”
Wygenerować i zbadać krzywe miareczkowania układów „symetrycznych” i skomentować zauważone prawidłowości.
Rozwiązanie zawierają arkusze Lab_24a>Przykład_1a/..d. Założono najprostszą formę równań reakcji połówkowych.
(9a)
(9b)
W obu przypadkach potencjały formalne są niezależne od pH roztworu i równe potencjałom standardowym. Symulacje wykonano dla wartości
oraz
co odpowiada miareczkowaniu oksydymetrycznemu.
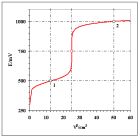
Na rys. 1 przedstawiono krzywą dla zL = zP = 1 i stechiometrycznych stężeń
.
Sprawdzamy, że EPR = 750 mV odpowiada obliczonemu ze wzoru (8). W PR występuje znaczny „skok potencjału”. Po dodaniu roztworu titranta w ilości równej połowie ilości niezbędnej do do osiągnięcia PR potencjał
.
i krzywa miareczkowania ma punkt przegięcia (1), natomiast po dwukrotnym przemiareczkowaniu (2) potencjał
.
(bez punktu przegięcia). Jest to konsekwencja wzorów ([3] – 11). Dla tak dużej różnicy potencjałów formalnych reakcja (6) przebiega „niemal do końca” czyli stężenia reagentów nie wziętych w nadmiarze są pomijalnie małe. W punkcie (1) mamy więc równość stężeń [RL] = [UL], natomiast w punkcie (2) [UP] = [RP] co dla jednostkowych współczynników i wzoru ([3] – 11)
(10)
daje opisaną prawidłowość niezależnie od liczb ładunkowych obu reakcji połówkowych, co potwierdzają krzywe miareczkowania. Czytelnik zapozna się z nimi samodzielnie i sprawdzi, że opisana prawidłowość nie wymaga „stechiometrycznego” stężenia roztworu titranta (arkusze Lab_24a> Przykład_1b/c/d).
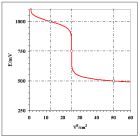
Na rys. 2 przedstawiono krzywą miareczkowania reduktometrycznego (arkusz Lab_24a>Przykład_1e); i w tym przypadku obserwuje się opisane prawidłowości.
Przygotowane na wymienionych arkuszach symulacje umożliwiają „zoom” czyli badanie krzywej miareczkowania w dostatecznie małym (wybranym przez Użytkownika) przedziale objętości roztworu titranta oraz wykreślenie pochodnej
.
, która jest dobrą miarą „ostrości skoku potencjału” .
Przykład 2. Krzywe miareczkowania układów modelowych – układy „niesymetryczne”
Wygenerować i zbadać krzywe miareczkowania dla układów „niesymetrycznych” i skomentować zauważone prawidłowości.
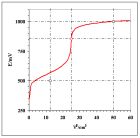
Rozwiązanie zawierają arkusze Lab_24a>Przykład_2a/..d. dla wartości potencjałów formalnych i stężeń takich jak w przykładzie 1. Na rys. 3a przedstawiono krzywą miareczkowania dla równań reakcji połówkowych.
(11a)
(11b)
Potencjał w PR równy 853,1 mV jest znacznie większy od obliczonego ze wzoru (8) a potencjał w punkcie przegięcia jest większy od
.
.
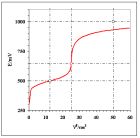
Na rys. 3b przedstawiono krzywą miareczkowania dla równań reakcji połówkowych.
(12a)
(12b)
W tym przypadku potencjał w PR równy 646,9,1 mV jest znacznie mniejszy od obliczonego ze wzoru (8) i zdeformowaniu uległa krzywa na prawo od PR. Pozostałe arkusze zawierają dalsze kombinacje współczynników stechiometrycznych – Czytelnik zapozna się z nimi i samodzielnie sformułuje wnioski. Ogólnie dla układów niesymetrycznych równanie (8) nie może być stosowane.
Przykład 3. Krzywe miareczkowania układów modelowych – wpływ różnicy potencjałow formalnych na krzywą miareczkowania
Wygenerować i zbadać krzywe miareczkowania np. dla układów „symetrycznych” dla różnych wartości różnicy potencjałów formalnych i skomentować zauważone prawidłowości.
Rozwiązanie zawierają arkusze Lab_24a>Przykład_3a/..f. dla reakcji połówkowych.
(13a)
(13b)
Na rys 4a/b/c przedstawiono krzywe dla różnic potencjałów formalnych równych 500, 250 oraz 100 mV. Wykreślono też stężenia poszczególnych reagentów w funkcji objętości roztworu titranta. Wnioskujemy, że różnica potencjałów formalnych rzędu 500 mV zapewnia „dobrze wykształconą” krzywą miareczkowania i przesunięcie równowagi reakcji (6) praktycznie „do końca na korzyść produktów”. Różnica tylko 100 mV jest zdecydowanie zbyt mała – w stanie równowagi współistnieją porównywalne ilości wszystkich reagentów, czego konsekwencją jest „nieczytelna krzywa miareczkowania”. Czytelnik samodzielnie przeprowadzi symulację dla innych liczb ładunkowych reakcji połówkowych i sprawdzi jak zwiększenie liczby ładunkowej jednej lub obu reakcji wpływa na relację między różnicą potencjałów formalnych a „wykształceniem krzywej miareczkowania”.
Przykład 4. Krzywe miareczkowania układów rzeczywistych – cerometria
Cerometria polega na miareczkowaniu mianowanym roztworem siarczanu(VI) ceru(IV) roztworu oznaczanego reduktora. Wykonać symulację krzywej miareczkowania cerometrycznego roztworu soli żelaza(II).
Symulację zawierają arkusze „Lab_24b>Przykład_4a/b. Wobec reakcji połówkowych
(14a)
(14b)
reakcji sumarycznej
(14c)
oraz różnicy potencjałów formalnych 900 mV otrzymujemy „dobrze wykształconą” krzywą miareczkowania jakościowo identyczną z przedstawioną na rys. 4a. Zwracamy uwagę, że potencjały formalne reakcji (14a/b) są niezależne od pH roztworu. Wobec „symetrycznych” równań reakcji (14a/b) prawdziwa pozostaje relacja (8). Czytelnik zapozna się z symulacją na wymienionych arkuszach.
Przykład 5. Krzywe miareczkowania układów rzeczywistych – manganometria (I)
Manganometria polega na miareczkowaniu mianowanym roztworem manganianu(VII) potasu (pot. nadmanganianu) roztworu oznaczanego reduktora w środowisku kwaśnym. Wykonać symulację krzywej miareczkowania manganometrycznego roztworu soli żelaza(II).
Symulację zawierają arkusze „Lab_24b>Przykład_5a/..d. Wobec reakcji połówkowych
(15a)
(15b)
otrzymujemy równanie reakcji sumarycznej
(15c)
Zwracamy uwagę, że potencjał formalny reakcji (15b) jest malejącą funkcją pH; dla pH równego odpowiednio 1 i 5 jest on odpowiednio równy 1436 oraz 1058 mV. Przebieg krzywych miareczkowania przedstawiono na rys. 5a/b; wnioskujemy że „dobrze wykształconą krzywą miareczkowanie” można otrzymać jedynie w środowisku dostatecznie kwaśnym. Czytelnik zapozna się z symulacją na wymienionych arkuszach i potwierdzi stosowalność wzoru (8)..
Przykład 6. Krzywe miareczkowania układów rzeczywistych – manganometria (II)
Nadtlenek wodoru można oznaczać manganometrycznie w środowisku kwaśnym. Wykonać symulację odpowiedniej krzywej miareczkowania.
Symulację zawierają arkusze „Lab_24b>Przykład_6a/..d. Wobec reakcji połówkowych
(16a)
(16b)
otrzymujemy równanie reakcji sumarycznej
(16c)
Potencjały formalne reakcji (16a/b) są malejącymi funkcjami pH. Czytelnik zapozna się z symulacjami na arkuszach Lab_24b>Przykład_6a/..d i sprawdzi, że otrzymujemy „dobrze wykształcone” krzywe miareczkowania jednak EPR nie może być obliczany ze wzoru (8) gdyż O2 (czyli UL) nie jest składnikiem roztworu.
Przykład 7. Krzywe miareczkowania układów rzeczywistych – chromianometria
Chromianometria polega na miareczkowaniu mianowanym roztworem dichromianu(VI) potasu roztworu oznaczanego reduktora w środowisku kwaśnym. Wykonać symulację krzywej miareczkowania chromianometrycznego roztworu soli żelaza(II).
Symulację zawierają arkusze „Lab_24b>Przykład_7a/b. Wobec reakcji połówkowych
(17a)
(17b)
otrzymujemy równanie reakcji sumarycznej
(17c)
Czytelnik zapozna się z krzywymi miareczkowania na wskazanych arkuszach. Należy zwrócić uwagę, że potencjał formalny reakcji (17b) jest malejącą funkcją pH oraz, że nie jest to reakcja „symetryczna” co wyklucza stosowanie wzoru (8) do obliczenia EPR.
Przykład 8. Krzywe miareczkowania układów rzeczywistych – oznaczanie manganu metodą Volharda
Metodę i właściwy dobór równań reakcji połówkowych omówiono na początku niniejszego artykułu; symulację zawierają arkusze Lab_24b>Przykład_8a/b. Czytelnik zapozna się z nimi samodzielnie.
Na tym zakończony zostanie cykl poświecony symulacjom reakcji utleniania – reduk¬cji. Zainteresowany Czytelnik może kontynuować symulacje interesujących do procesów sa¬mo¬dzielnie modyfikując przygotowane arkusze.
Struktura folderów i kopiowanie skoroszytów
Komplet plików jest „spakowany” w archiwum *.zip i Czytelnik musi go rozpakować po „ściągnięciu” na dysk twardy swojego peceta. Optymalne wydaje się następujące postępowanie:
Na dysku twardym swojego „peceta” należy utworzyć następującą strukturę folderów:
Z kolei należy odszukać stronę internetową (www.lab.media.pl); znajduje się na niej „link” na stronę „Obliczenia i symulacje za pomocą arkusza MS Excel”; po przejściu na nią można przystąpić do skopiowania plików dołączonych do niniejszego artykułu. W tym celu należy (przeglądarka Internet Explorer):
- Kliknąć prawym klawiszem myszki nazwę pliku Lab_24.zip po czym w otwartym oknie menu lokalnego wybrać usługę „Zapisz cel jako ...”
- Odszukać na dysku swojego „peceta” folder LABEXCELROBOCZY i potwierdzić [OK]
- Rozpakować archiwum Lab_24.zip w folderze ROBOCZY
- Przenieść pliki do odpowiednich folderów (patrz schemat folderów)
- Otworzyć arkusz MS Excel i zainstalować w nim dodatek Labredox.xla zgodnie z instrukcją podaną w artykule zamieszczonym w LAB, 6, (2001). Jeżeli Czytelnik korzysta już z oprogramowania i skoroszytów z przykładami pochodzących z poprzednich artykułów, to oczywiście może je pozostawić w istniejących folderach (nie ma konfliktów nazw plików).
Literatura
- W. Ufnalski, Symulacja równowagi utlenienia – redukcji za pomocą MS Excela I – Potencjały reakcji połówkowych i ich interpretacja, LAB, (2006), 1, 41 – 48.
- W. Ufnalski, Symulacja równowagi utlenienia – redukcji za pomocą MS Excela II – Diagramy trwałości elektrochemicznej „potencjał – pH” i ich interpretacja, LAB, (2006), 3, 30 – 43.
- W. Ufnalski, Symulacja równowagi utlenienia – redukcji za pomocą MS Excela III – Obliczanie równowag utleniania - redukcji, LAB, (2007), 2, 31 – 38.
- J. Minczewski, Z. Marczenko, Chemia analityczna, PWN, Warszawa, 1973.
- R. Brdiczka, Podstawy chemii fizycznej, PWN, Warszawa, 1970.
*dr inż. Waldemar Ufnalski; Zakład Chemii Fizycznej, Wydział Chemiczny - Politechnika Warszawska; waldemar@ch.pw.edu.pl
Rys. 1. Krzywa miareczkowania oksydymetrycznego układu modelowego (opis w tekście przykładu 1)
Rys. 2. Krzywa miareczkowania reduktometrycznego układu modelowego (opis w tekście przykładu 1)
3a)
3b)
Rys 3. Krzywa miareczkowania układów modelowych „niesymetrycznych” dla równań reakcji połówkowych odpowiednio: a) (11a/b) oraz b) (12a/b). Przyjęto , oraz stechiometryczne stężenia roztworów 0,1000 mol•dm-3.
4a)
 4b)
4b)
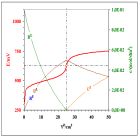 4c)
4c)

Rys. 4. Krzywa miareczkowania układów modelowych „symetrycznych” dla równań reakcji połówkowych (13a/b). Przyjęto stechiometryczne stężenia roztworów 0,1000 mol•dm-3 oraz
i równe odpowiednio a) 1000 mV, b) 750 mV oraz c) 600 mV.
5a)
 5b)
5b)

Rys. 5. Krzywe miareczkowania manganometrycznego oznaczania żelaza(II) dla wartości pH równych odpowiednio 1,0 (a) oraz 5,0 (b). Przyjęto stechiometryczne stężenia roztworów równe odpowiednio 0,1000 mol•dm-3 oraz 0,02000 mol•dm-3 .
wstecz
Podziel się ze znajomymi










